Ecuaciones Diferenciales: 4.2.2 Utilizando la Transformada de Laplace

martes, 26 de junio de 2012

4.2.2 Utilizando la Transformada de Laplace

La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, o en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la funciónF(s), definida por:

$F(s) = \mathcal{L} \left\{f(t)\right\} =\int_{0}^\infty e^{-st} f(t)\,dt.$

siempre y cuando la integral esté definida. Cuando f(t) no es una función, sino una distribución con una singularidad en 0, la definición es

$F(s) = \mathcal{L} \left\{f(t)\right\} =\lim_{\varepsilon \rightarrow 0} \int_{-\varepsilon}^\infty e^{-st} f(t)\,dt.$

Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:

$F_B(s) = \mathcal{L}\left\{f(t)\right\} =\int_{-\infty}^{\infty} e^{-st} f(t)\,dt.$

La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).
$\mathcal{L}$ es llamado el operador de la transformada de Laplace.

PROPIEDADES

Linealidad $\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}$

Derivación

$\mathcal{L}\{f'(t)\} = s \mathcal{L}\{f(t)\} - f(0)$

$\mathcal{L}\{f''(t)\} = s^2 \mathcal{L}\{f(t)\} - s f(0) - f'(0)$

$\mathcal{L}\left\{ f^{(n)}(t) \right\} = s^n \mathcal{L}\{f(t)\} - s^{n - 1} f(0) - \cdots - f^{(n - 1)}(0)$ =

= $\mathcal{L}\left\{ f^{(n)}(t) \right\} = s^n \mathcal{L}\{f(t)\} - \sum_{i=1}^{n} s^{n - i} f^{(i - 1)}(0)$

Integración

$\mathcal{L}\left\{ \int_0^t f(\tau)\, d\tau \right\} = {1 \over s} \mathcal{L}\{f\}$

Dualidad

$\mathcal{L}\{ t f(t)\} = -F'(s)$

Desplazamiento de la frecuencia

$\mathcal{L}\left\{ e^{at} f(t) \right\} = F(s-a)$

Desplazamiento temporal

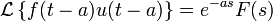
$\mathcal{L}\left\{ f(t - a) u(t - a) \right\} = e^{-as} F(s)$

$\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\} = f(t - a) u(t - a)$

Desplazamiento potencia n-ésima

$\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]$

Convolución

$\mathcal{L}\{f*g\} = \mathcal{L}\{ f \} \mathcal{L}\{ g \}$

Bibliografia

Ecuaciones Diferenciales, Deniss G. Zill, Lenguaje Learning

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)